The distributive property of multiplication is just one of those math topics that 3rd graders struggle with. And you know what that means … it’s a frustrating topic to teach! For years I remember dreading the lesson on the distributive property of multiplication because I knew what was coming 😭 It seemed like no matter what I tried, my students just weren’t getting it!

That all changed once I introduced my kids to the Distributive Doctor + started implementing a 3 step approach known as CRA.
What is CRA?
Concrete Representational Abstract or CRA is an instructional approach that begins with students using manipulatives, progresses to them making drawings, and ends with students solving problems using only numbers and symbols. The purpose of using this approach is to make sure students gain a thorough understanding of the distributive property of multiplication.
What does the CONCRETE STAGE look like?
The concrete level is known as the “doing stage”… This is the level kids love the most! It’s when they get to use manipulatives or counters to “break apart” arrays.

I usually begin my lesson on the distributive property of multiplication by telling the students that we are all going to be doctors for the day. Surgeons to be exact… I explain that we will “operate” on arrays. This usually motivates the kids and gets their attention!

Our “surgery” begins with students rolling dice to determine the initial multiplication problem. In this example, they roll a 4 and 5 so we record the problem 4×5 up top. Next, they create a 4×5 array using blue beads. Using a popsicle stick as their “scalpel”, they “break apart” the array into two smaller arrays. Students then use additional color beads to create the two separate arrays 4×3 and 4×2.

It’s important for students to understand that when you break apart an array nothing is being added or taken away from the array. the total number of beads remains the same. At this point I also have students circle the factor that gets broken apart. In this case, we circle the 5 which is broken up into the addends 3 and 2. This simple step makes it easier for kids to progress to the next two stages.
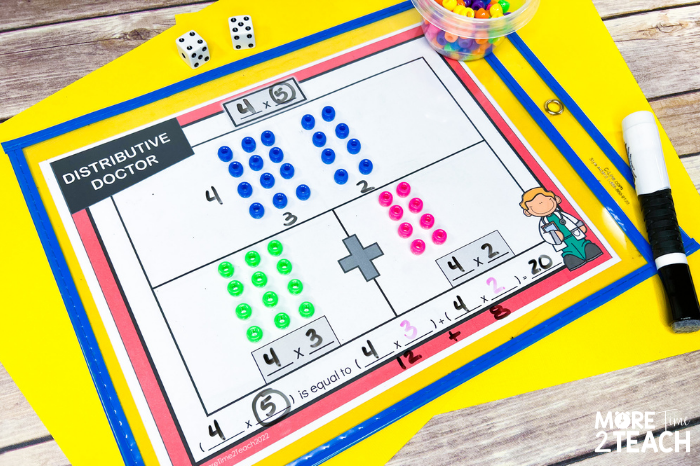
The final step involves creating an equation. Through discussions ask students what they notice about the arrays they created. You want them to realize that the factor 4 was left untouched and so each array created also has a 4 as a factor. Likewise, their equation will have a 4. Next, you want them to realize that the 3 and 2 comes from the factor 5 being broken apart. In the beginning, have students use a different color for the numbers they broke apart. Once they develop more understanding of the distributive property of multiplication, they’ll no longer need that support.
What does the Representational Stage look like?
The representational level is known as the “seeing stage”… This level involves using images to represent objects to solve problems.
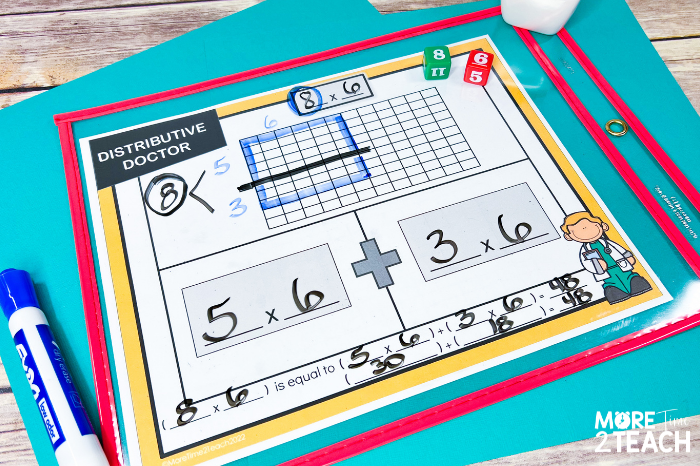
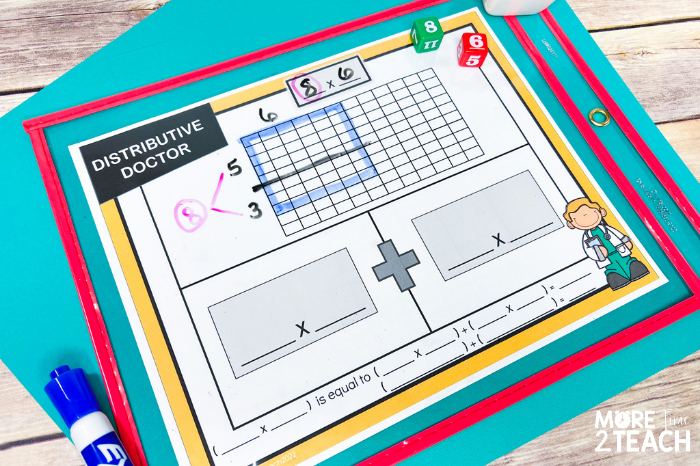
Similar to the previous stage, students begin by rolling dice to determine the initial multiplication problem. In this example, they roll an 8 and 6 so we record the problem 8×6 up top. Next, they create an array on the grid.

For this break apart “surgery”, students use a marker. This time they “break apart” the array by drawing a line dividing it into two smaller arrays. Then they label the sides of their arrays and show the sum of the two addends which equals 8… the circled number they broke apart.
Students then record the expressions 5×6 and 3×6 representing the two arrays created. It’s at this time that I point out that in the expressions the factor that was not affected by the “surgery” stays the same. That’s why both equations have a 6 as a factor. On the other hand, the factor that is broken apart (8) is replaced by the addends that make up its sum (5 and 3).
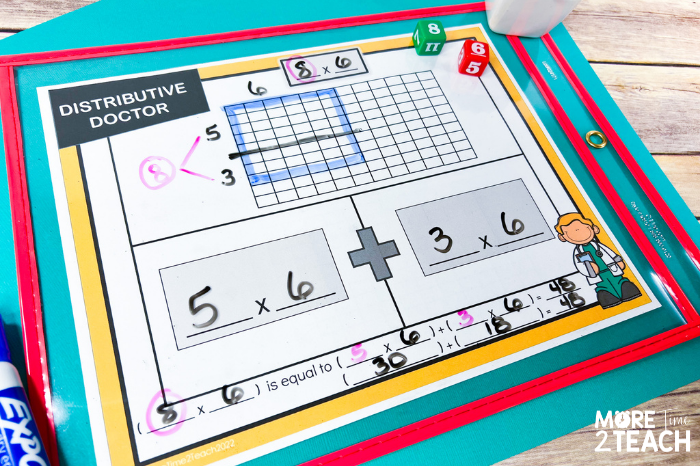
Once again the final step involves creating an equation similar to the ones they created in the concrete stage.
What does the Abstract Stage look like?
The abstract level is known as the “symbolic stage”… this level involves using only numbers and symbols to solve problems.

By the time the students reach this final stage they are more familiar with writing equations. As in the previous two stages of CRA instruction, I have them circle the factor they choose to break apart. Later on, students become more confident and can skip this step.

Finally, they record expressions demonstrating the distributive property of multiplication. Once you see your students gaining confidence, bump things up a notch by giving them challenging problems to break apart such as 4×18 or 8×16. You can also differentiate by having them write 2 different equations demonstrating the distributive property of multiplication. The mats I use are double-sided. One side has the simpler equations and then the other side is more advanced with 2 different equations. This comes in handy when you need that differentiation for students that catch on quicker.
Download the Distributive Dr. work mats here
To get these math mats for FREE just enter your email down below. Each mat comes in 2 versions making them perfect for differentiated instruction and small groups.
Looking for more help teaching the Distributive Property of Multiplication?
If you and your students enjoy these Distributive Property of Multiplication math mats you will love this bundle. The Distributive Property bundle includes multiple activities for the concrete, representational, and abstract stages of instruction, a hands-on project that makes a great classroom display, 44 task cards focusing on the distributive property, and assessments. This bundle also includes a digital component perfect for distance learning!





No Comments